The Maths Orgy Thread
-
It's been suggested a couple of times, so here goes, a new home for your favourite formula, lemma, theorem or statistician.
If you're really well behaved, I may even pose a "problem of the week". But only if you have behave well.
A couple of my faves then:
Euler's identity
A mathematical classic. But a genuine WTAF when you first learn it. It's still hard to imagine how three numbers, one of which is imaginary, can cancel each other out so elegantly. Arguably the photo doesn't do it justice.
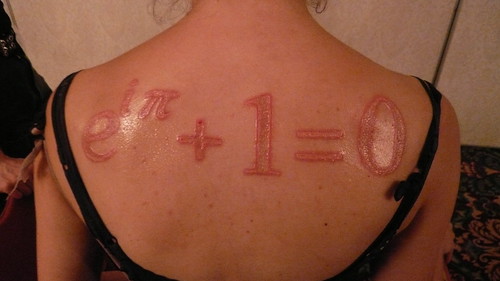
There's loads of other crazy stuff with exponents and sequences. And fourier shizzle. But not for today, as you haven't been good enough.
Next up, Liouville's theorem:
Any bounded, entire (differentiable-everywhere) function must be constant. (This refers to 'complex' numbers, i.e. C->C.)
i.e. there's nothing like a sin wave, which is bounded, differentiable everywhere, but not constant, if you treat it over the whole complex plane. (The sin function goes a bit ape if you start doing it on imaginary numbers, so isn't bounded.)
That's another one that, to be, just defies expectation.
What else then?
Last for today, the Central Limit Theorem:
If you take _any_ probability distribution, and sample from it enough times, you end up with the normal distribution.
Madness.
Anyway, hope you're having fun. Do add your own faves, or ask questions, or tell me to get a life. -
69 to the power of 69. Am I doing it right?
-
Ish
-
I find the identity a bit of a swizzy cheat.
Firstly because the 0 is shoehorned in there by rearrangement.
Secondly couldn't the pi be replaced by any number if you chose the appropriate number of degrees in a circle? Say if a full rotation equalled 4 then it would be e^2i = -1? -
mistercrayon wrote:I find the identity a bit of a swizzy cheat.
Firstly because the 0 is shoehorned in there by rearrangement.
Secondly couldn't the pi be replaced by any number if you chose the appropriate number of degrees in a circle? Say if a full rotation equalled 4 then it would be e^2i = -1?
Besides being wrong, you're missing the point.
-
There is a point? Elaborate please. I'm interested.I am a FREE. I am not MAN. A NUMBER.
-
SpaceGazelle wrote:
Besides being wrong, you're missing the point.mistercrayon wrote:I find the identity a bit of a swizzy cheat. Firstly because the 0 is shoehorned in there by rearrangement. Secondly couldn't the pi be replaced by any number if you chose the appropriate number of degrees in a circle? Say if a full rotation equalled 4 then it would be e^2i = -1?
The first one is definitely true. The rearrangement is clearly there for maths people to Jizz over. Nobody writes 2+3-5 = 0.
The latter I'm unsure about. Seems logical to me. sin x + cos x = circle whatever angular system you use right? -
Yeah pi isn't a "choice" for the number of degrees in a (half) circle, it has a precise definition and reason. If you choose a different scale, then not only does the equality not hold up, other nice things stop working too. E.g. the area of a slice of a circle of x radians is given by A=rx. If you choose a different scale, then the area doesn't have such a neat formula, it needs some other scale factor.
E.g. you say there are 4 'crayons' in a circle, and the angle x is measured in crayons, then A=rx*(pi/2) or something.
And e^2i doesn't magically become -1 just because 'crayons' exist as a new unit, all the complex number stuff depends on it having the precise value it has.
(I agree about the being shoehorned in though: I normally prefer it as e^ipi = -1, but meh) -
I did all this in the Maroon Room about this exact equation. On phone so I'll be brief.
It tells us that there is a direct relationship between several fundamental constants, and that imaginary numbers are part of that relationship, and that relationship is true and proved in the tightest sense. It tells us there is perhaps a deeper truth of why these constants might be related, and that truth connects constants and mathematics im ways not understood. It hints that reality is made of mathematics, not described by it. -
In short, there is no fucking way that equation should exist, not unless something seriously fucking mental is going on that is not yet understood.
-
I've never got passed thinking that "made of mathematics" vs. "described by mathematics" was just obtuse use of language. The various snippets I've read on that topic don't really convince me it's a concept to get excited about, more just a different way of viewing e.g. physics (by saying the equations are the reality, the empirical stuff is just sampling those equations).
By I know you're kind of an advocate SG, so do provide more linkies.
I absolutely believe there's some very fundamental beauty to mathematics, things intertwining in magical ways though. And in ways that are just "there" in some sense, rather than require human imagination to exist. Is that the same thing? I don't think it is quite.
Well, that was even less coherent than I expected.... -
And yeah, e and i are equally not-chosen-at-random.
e has the magic property that if you draw the graph y=e^x, the angle of the line at any point precisely matches the value y value. No other number has that property. (Well, except 0 I guess .)
.) -
(e to the i.pi) + 1 = 0 is indeed beautiful, and as said above - deeply profound. It blew my mind when I first came across it. Would that have been in A level?
I'm more a fan than a practitioner. I only studied maths to year 1 in university when I had to take it as part of my Computer Science degree. I recently took an OU year 1 maths course and enjoyed it immensely and I found that stuff I has hazy on at A level and year 1 university actually quite easy.
I always had a blind spot about using the equations of motion for some reason and found them easy on the OU unit. Vector maths too -ships heading on bearings described as a vector and calculating directions after adding the wind vector in. All simple but immensely rewarding.
I have pi memorised to 50-odd places. Decided to do it when I was 17 to wind a guy up in class who had it done to 20. I can still recall it on demand. Weird.Holding the wrong end of the stick since 2009. -
Can someone explain this e iPie thing to a layman? The wiki page on it may as well have been written in sanskrit.
-
On phone so no links. Not sure if there are links tbh. There are no particles and there are no waves, there is only equations and constants
-
I only appreciated it at a mechanical level. You can express (e ^ ab) as a sum of sin b and a.cos b (or something like like that) and it all reduces down to -1 when you substitute i and pi in for a and b.
It is quite profound. The fact that the square root of -1 - an imaginary construct that has practical applications, shares a relationship with two numbers that pop up in nature (pi and e) and the two numbers you need to generate all integers (0 and 1) is just fucking cool.
http://en.wikipedia.org/wiki/Euler's_identityHolding the wrong end of the stick since 2009. -
What is this wizardry and where may a chump like me (who has barely dabbled in trig) learn more of it?
I got Flatland the other week (not started it yet though), so something like that?
On that note, is that Godel Escher Bach or whatever it is book worth a gander? Ta! -
There are "popular" maths books around. I have a few I picked up cheap.
"17 equations that changed the world" is one - quite readable. Though there is a piece on topology that turned my head inside out (pun unintended) and I skipped that chapter....Holding the wrong end of the stick since 2009. -
Singh on Fermat is readable.
-
Also his book on cryptography.
-
The Fermat book is a good read - more of human story though. The maths around the proof is beyond all but a small % of the world's population I suspect.
The mystery of the Fermat proof by Wiles is that it is a 20thC proof - and it is unlikely Fermat's proof is the same.Holding the wrong end of the stick since 2009. -
If he had a proof...
-
Well it's clear Fermat didn't have a proof never mind an elegant one. But it's a great book. If I recall it goes wider than Fermat and looks at other unsolved problems? (Maybe?)
-
Think you're right. It's been a while now. Stuff like the 4 colour problem may have got a mention.
Quite possible Fermat was bullshitting or mistaken.....?Holding the wrong end of the stick since 2009. -
Or drunk.
-
That would be splendid.....300 odd years of work based on a drunken boast.Holding the wrong end of the stick since 2009.
-
acemuzzy wrote:And yeah, e and i are equally not-chosen-at-random. e has the magic property that if you draw the graph y=e^x, the angle of the line at any point precisely matches the value y value. No other number has that property. (Well, except 0 I guess
 .)
.)
I think there must have been a number with this property. The fact we find that property interesting is surely how you end up finding e. -
Its stuff like this that really got me interested in maths and physics before I ran up against the limits of my own limited facility with them and my lack of patience for undertaking the hard graft in learning that would provide any real understanding.SpaceGazelle wrote:I did all this in the Maroon Room about this exact equation. On phone so I'll be brief.
It tells us that there is a direct relationship between several fundamental constants, and that imaginary numbers are part of that relationship, and that relationship is true and proved in the tightest sense. It tells us there is perhaps a deeper truth of why these constants might be related, and that truth connects constants and mathematics im ways not understood. It hints that reality is made of mathematics, not described by it.
-
I like (but dont entirely grasp) the concept of cardinality and different sized infinities. Also the concept of the Infinite Hotel where a new guest arrives and every room is already occupied.
The Euler identity is a classic too. I just like telling someone that X^2 +1 = 0 has a solution and the moment of realisation there is such a thing as imaginary numbers."Sometimes it's better to light a flamethrower than curse the darkness." ― Terry Pratchett -
mistercrayon wrote:acemuzzy wrote:And yeah, e and i are equally not-chosen-at-random. e has the magic property that if you draw the graph y=e^x, the angle of the line at any point precisely matches the value y value. No other number has that property. (Well, except 0 I guess
 .)
.)
I think there must have been a number with this property. The fact we find that property interesting is surely how you end up finding e.
Yeah it all ties into the Taylor expansion of e^x, sin (x) and cos (x).
e=1+1/2!+1/3!+1/4!+...
Eulers thing becomes "obvious" when you understand the re^i theta representation of complex numbers.
I need my pc...
-
SpaceGazelle wrote:On phone so no links. Not sure if there are links tbh. There are no particles and there are no waves, there is only equations and constants
That doesn't mean it's not useful to talk about particles and waves though
Howdy, Stranger!
It looks like you're new here. If you want to get involved, click one of these buttons!
Categories
- All Discussions2,713
- Games1,877
- Off topic836







